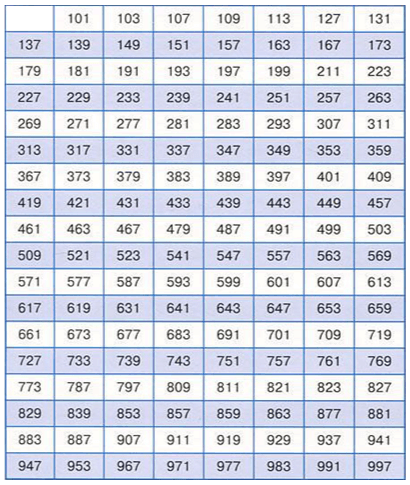
В таблице простых чисел возможно заметить интересную закономерность — одни числа выделены черным цветом, а другие красным. Это явление не случайно и имеет свои тайны и секреты. Рассмотрим подробнее, почему некоторые числа красные, а другие черные.
Оказывается, цветовая графика в таблице простых чисел имеет глубокий смысл и отражает важные свойства чисел. Красные числа обладают особенностью, которая их отличает от черных чисел. Они являются простыми числами, то есть числами, которые делятся только на 1 и на себя самого. Простые числа играют важную роль в теории чисел и имеют множество приложений в криптографии и алгоритмах шифрования.
Черные числа, напротив, составляют противоположность красным числам. Они являются составными числами, то есть числами, которые имеют делители помимо 1 и самого себя. Черные числа могут быть разложены на простые множители, что делает их менее «особенными» с точки зрения теории чисел.
Таким образом, цветовая графика в таблице простых чисел не только сделана для эстетического восприятия, но и содержит в себе глубокий смысл и информацию о свойствах чисел. Она помогает визуализировать различия между простыми и составными числами и помогает исследователям и математикам в их работе с числами и их свойствами.
Почему некоторые числа в таблице простых чисел черные, а другие красные?
Черные числа в таблице обозначают составные числа, то есть числа, которые имеют делители помимо 1 и самого себя. Эти числа не являются простыми и могут быть разложены на простые множители.
С другой стороны, красные числа представляют простые числа — числа, которые имеют только два делителя: 1 и само число. Красный цвет помогает выделить эти числа и облегчить их визуальное нахождение в таблице.
Использование цветовой графики в таблице простых чисел позволяет сделать ее более наглядной и помогает лучше понять свойства чисел. Это удобно, например, при поиске простых чисел, исследовании и анализе числовых последовательностей.
Секреты цветовой графики
Одни числа в таблице простых чисел обозначены черным цветом, а другие — красным. Черные числа обозначают простые числа, то есть числа, которые делятся только на 1 и на себя самого. Красные числа, напротив, обозначают составные числа, то есть числа, которые имеют делители помимо 1 и самого себя.
Такой цветовой код позволяет наглядно выделять простые числа в таблице и отличать их от составных чисел. Это особенно полезно при больших объемах данных, когда нужно быстро находить и анализировать простые числа.
Кроме того, цветовая графика может использоваться для обозначения других характеристик чисел. Например, разные оттенки красного цвета могут обозначать различные типы составных чисел, такие как полные квадраты или числа с множителями в определенном диапазоне.
Таким образом, цветовая графика в таблице простых чисел — это мощный инструмент для визуализации данных и облегчения анализа чисел. Она позволяет быстро и наглядно выделять и исследовать простые числа, а также обозначать другие важные характеристики чисел.
Что влияет на цветовое обозначение чисел в таблице простых чисел?
Одна из основных характеристик числа, влияющая на его цветовое обозначение, — его простота. Простые числа, которые делятся только на себя и на единицу без остатка, обозначены красным цветом. Они считаются особыми и имеют важное значение в математике. Красные числа обладают свойствами, которые делают их основными строительными блоками числовой системы.
Черные числа в таблице простых чисел обозначают составные числа, которые могут быть разложены на простые множители. Это числа, которые делятся на другие числа помимо себя и единицы. Черные числа можно считать комбинациями красных чисел, их «строительными элементами».
Еще одним фактором, определяющим цветовое обозначение чисел, может быть их значение. Например, можно использовать цвета для выделения определенных классов чисел, таких как простые числа-близнецы (числа, разделенные друг на друга всего одним числом), простые числа-близнецы, сумма которых равна простому числу и т.д.
Цветовое обозначение чисел в таблице простых чисел не только делает ее более наглядной и интересной, но и отражает глубину и сложность числовой системы. Благодаря цветам, можно легче видеть и анализировать математические закономерности и связи между числами, а также проникнуть в тайны простых чисел.
Какой цвет какое число обозначает?
Черный цвет обычно используется для обозначения простых чисел. Простые числа — это натуральные числа, которые имеют только два делителя: единицу и само число. В таблице они выделены черным цветом, чтобы легче было идентифицировать их среди других чисел.
Красный цвет, с другой стороны, используется для обозначения чисел, которые не являются простыми. Это могут быть составные числа, которые имеют более двух делителей, или числа, обладающие определенными свойствами, которые отличают их от простых чисел. Например, красным цветом могут быть выделены числа, которые являются степенями других чисел или числа Фибоначчи.
Таким образом, цветовая графика в таблице простых чисел помогает визуально различать разные типы чисел и облегчает их анализ и использование в математических вычислениях и исследованиях.
Почему это важно?
Цветовая графика таблицы простых чисел не только делает ее более привлекательной визуально, но и имеет важное значение с точки зрения визуализации и анализа данных.
Различные цвета в таблице простых чисел помогают нам легко выделять определенные числа и паттерны. Например, красный цвет может использоваться для выделения простых чисел, которые имеют особую важность или интерес для исследователей. Это позволяет нам быстро и легко идентифицировать их и анализировать их свойства.
Кроме того, цветовая графика может помочь нам визуализировать различные характеристики простых чисел. Например, мы можем использовать разные оттенки или яркость цветов для отображения различной степени простоты чисел или их связи с другими числами. Это может помочь исследователям выявить закономерности и установить связи между числами быстрее и эффективнее.
Кроме того, цветовая графика позволяет визуализировать большие объемы данных и сделать их более понятными и доступными. Вместо изучения большой таблицы чисел, мы можем сразу видеть образцы и структуру простых чисел благодаря цвету. Это помогает сократить время анализа и облегчить понимание сложных математических концепций.
В целом, цветовая графика таблицы простых чисел играет важную роль в визуализации и анализе данных. Она помогает нам выделять и исследовать важные числа и паттерны, а также упрощает визуализацию и понимание больших объемов данных. Это делает таблицу простых чисел более доступной и полезной для математиков и научных исследователей.
Роль цветовой графики в понимании таблицы
Цветовая графика в таблице простых чисел играет важную роль в поддержании и улучшении понимания информации. Когда мы смотрим на таблицу, на первый взгляд может показаться, что цвета применяются просто для украшения или разнообразия. На самом деле, каждый цвет имеет свой смысл и выполняет свою функцию, помогая нам анализировать данные.
Черный цвет используется для обозначения простых чисел. Это позволяет нам легко идентифицировать эти числа и выделять их в таблице. Кроме того, черный цвет обычно ассоциируется с основными и важными элементами, поэтому он создает впечатление устойчивости и надежности. Благодаря этому, таблица простых чисел выглядит структурированной и организованной.
Красный цвет, с другой стороны, используется для выделения особых чисел, таких как числа-близнецы или числа Фибоначчи. Этот яркий цвет привлекает внимание и делает эти числа более заметными в контексте остальных простых чисел. Благодаря этому, мы можем быстрее обнаружить исторически значимые числа или интересные числовые закономерности.
Простые числа и их значения
Каждое простое число имеет свое уникальное значение, которое определяется его положением в таблице простых чисел. В таблице простых чисел часть чисел обычно обозначается черным цветом, а другая часть — красным.
Черные числа обозначают простые числа, которые имеют значение, кратное 10. Например, числа 10, 20, 30 и т. д. — все они являются черными числами.
Красные числа, с другой стороны, обозначают простые числа, которые не являются кратными 10. Это могут быть, например, числа 2, 3, 5, 7 и т. д. — все они являются красными числами.
Цветовая графика в таблице простых чисел помогает наглядно различить разные категории чисел и увидеть закономерности в их расположении. Это позволяет упростить анализ и использование простых чисел в математических вычислениях.
Практическое применение цветовой графики
Цветовая графика в таблице простых чисел имеет не только эстетическую ценность, но и широкий спектр практического применения. Вот несколько примеров, как цветовая графика может быть полезной:
- Визуализация данных: Цветовая графика позволяет визуально представить структуру и свойства простых чисел. С помощью различных цветов можно выделить определенные характеристики или особенности числовых последовательностей.
- Образование: Показывая цветами различные закономерности и связи между числами, цветовая графика может помочь в обучении математике. Ученикам будет проще понять простые числа и их свойства с помощью наглядного представления.
- Научные исследования: Цветовая графика может быть полезным инструментом при анализе простых чисел в научных исследованиях. Она помогает увидеть закономерности, распределение и свойства числовых последовательностей, что может привести к новым открытиям и развитию математической науки.
- Криптография: Простые числа играют важную роль в криптографии, и цветовая графика может помочь в анализе и выборе подходящих чисел для шифрования и дешифрования данных. Она может помочь в поиске особых закономерностей и связей между числами, что может быть полезно для создания надежных криптографических алгоритмов.
Таким образом, цветовая графика в таблице простых чисел имеет много практических применений и может быть очень полезным инструментом для анализа чисел, обучения и научных исследований. Она позволяет наглядно и эффективно представить данные о простых числах, облегчая их визуальное восприятие, а также способствуя развитию математической науки и криптографии.
Вопрос-ответ:
Почему в таблице простых чисел одни числа черные, а другие красные?
Цвета в таблице простых чисел указывают на их простоту. Черным цветом обозначаются составные числа, то есть числа, которые делятся на другие числа помимо 1 и самого себя. Красным цветом обозначаются простые числа, которые делятся только на 1 и самого себя.
Какая система используется для выбора цветов в таблице простых чисел?
В таблице простых чисел используется система цветовой графики, которая называется RGB (Red, Green, Blue). Каждый цвет представляется комбинацией трех основных цветов: красного, зеленого и синего. В зависимости от значения каждого из этих цветов формируется конечный цвет, который используется для обозначения числа в таблице.
Какие преимущества имеет использование цветовой графики в таблице простых чисел?
Использование цветовой графики в таблице простых чисел позволяет визуализировать простые и составные числа, что делает их классификацию и анализ более удобными. Благодаря цветам, можно сразу заметить простые числа в таблице и их распределение. Это упрощает работу с таблицей и облегчает поиск определенных числовых особенностей.
Какой алгоритм используется для определения цвета числа в таблице простых чисел?
Для определения цвета числа в таблице простых чисел используется алгоритм проверки на простоту. Каждое число последовательно проверяется на деление без остатка на все числа, начиная от 2 до корня из самого числа. Если число делится хотя бы на одно из чисел без остатка, оно считается составным и обозначается черным цветом. Если число не делится на все числа без остатка, оно считается простым и обозначается красным цветом.
Можно ли изменить цветовую схему в таблице простых чисел?
Да, цветовую схему в таблице простых чисел можно изменить. В зависимости от выбранного программного или графического инструмента, можно настроить свою цветовую палитру или использовать готовые схемы цветов. Но важно учитывать, что в общепринятой системе цветовой графики для таблицы простых чисел используется комбинация черного и красного цветов для обозначения простых и составных чисел соответственно.